Colisiones unidimensionales

Las colisiones entre partículas se pueden clasificar utilizando el coeficiente de restitución, el cual se define como la razón:$$e=-\frac{\vec{v}_{1f}-\vec{v}_{2f}}{\vec{v}_{1i}-\vec{v}_{2i}}=\begin{cases}e=1\hspace{1.46cm}\text{Elásticas}\\ \\0<e<1\hspace{0.908cm}\text{Inelásticas}\\ \\ e=0\hspace{1.47cm}\text{Totalmente Inelásticas}\\ \end{cases}$$donde $v_{1i}$ es la velocidad inicial de la primera partícula y $v_{1f}$ su velocidad después de la colisión. De manera similar, $v_{2i}$ y $v_{2f}$ corresponden a la velocidad inicial y final de la segunda partícula, respectivamente. A continuación, en la Fig. 1, se muestra una representación gráfica de este concepto.

Fig. 1. Tipos de colisiones.

Ejemplo 1 (Colisión unidimensional plástica). Considere dos partículas de masas $m_1$ y $m_2$ que se mueven con velocidades iniciales $\vec{v}_{1i}$ y $\vec{v}_{2i}$ a lo largo de la misma línea recta, como se muestra en la figura. Las dos partículas chocan de frente, quedan unidas y luego se mueven con alguna velocidad común $\vec{v}_f$ después de la colisión.

Fig. 2. Colisión unidimensional plástica.

Ya que la cantidad de movimiento de un sistema aislado se conserva en cualquier colisión, se puede decir que la cantidad de movimiento total antes de la colisión es igual a la cantidad de movimiento total del sistema compuesto después de la colisión:$$m_1\vec{v}_{1i}+m_2\vec{v}_{2i}=(m_1+m_2)\vec{v}_f,$$al despejar la velocidad final se obtiene:$$\vec{v}_f=\frac{m_1\vec{v}_{1i}+m_2\vec{v}_{2i}}{m_1+m_2}.$$Este resultado es clave para entender como funciona el péndulo balístico del ejemplo 2.

Ejemplos 2 (El péndulo balístico). Este es un aparato que se usa para medir la rapidez de un proyectil que se mueve rápidamente, como una bala. Un proyectil de masa $m_1$ se dispara hacia un gran bloque de madera de masa $m_2$ suspendido de unos alambres ligeros. El proyectil se incrusta en el bloque y todo el sistema se balancea hasta una altura $h$. ¿Cómo se determina la rapidez del proyectil a partir de una medición de $h$?

Fig. 3. Péndulo balístico.

Del resultado del ejemplo 1, se tiene:$$v_{B}=\left(\frac{m_1}{m_1+m_2}\right)v_{1A}.$$Ahora, la energía cinética total del sistema inmediatamente después del choque es:$$K_B=\frac{1}{2}\left(m_1+m_2\right)v^2_B,$$sustituyendo el valor de $v_B$, se obtiene la energía cinética en términos de la velocidad del proyectil$$K_B=\frac{m^2_1v^2_{1A}}{2\left(m_1+m_2\right)}.$$Y del principio de conservación de la energía:\begin{align*}K_B+V_B&=K_f+V_f\\ \frac{m_1^2v^2_{1A}}{2(m_1+m_2)}&=(m_1+m_2)gh,\end{align*}podemos, determinar la velocidad del proyectil despejando a $v_{1A}$:$$\boxed{v_{1A}=\left(\frac{m_1+m_2}{m_1}\right)\sqrt{2gh}.}$$
Ejemplos 3 (Colisiones unidimensionales elásticas). Considere dos partículas de masas $m_1$ y $m_2$ que se mueven con velocidades iniciales $\vec{v}_{1i}$ y $\vec{v}_{2i}$ a lo largo de la misma línea recta, como se muestra en la Fig. 4. Las partículas chocan frontalmente y luego dejan el sitio de colisión con diferentes velocidades $\vec{v}_{1f}$ y $\vec{v}_{2f}$. En una colisión elástica, tanto la cantidad de movimiento como la energía cinética del sistema se conserva.

Fig. 4. Colisión unidimensional elástica.

Por ende, al considerar velocidades a lo largo de la dirección horizontal en la figura, se tiene \begin{align*} m_1v_{1i}+m_2v_{2i}&=m_1v_{1f}+m_2v_{2f}\\
\frac{1}{2}m_1v^2_{1i}+\frac{1}{2}m_2v^2_{2i}&=\frac{1}{2}m_1v^2_{1f}+\frac{1}{2}m_2v^2_{2f}\end{align*}Si las masas y velocidades iniciales se conocen en ambas partículas. Las ecuaciones se pueden resolver para las velocidades finales mediante:\begin{align*}v_{1f}=\left(\frac{m_1-m_2}{m_1+m_2}\right)v_{1i}+\left(\frac{2m_2}{m_1+m_2}\right)v_{2i}\\v_{2f}=\left(\frac{2m_1}{m_1+m_2}\right)v_{1i}+\left(\frac{m_2-m_1}{m_1+m_2}\right)v_{2i}\end{align*}Veamos unos casos especiales de este tipo de colisiones.

Caso 1. Si $m_1=m_2$, las ecuaciones muestran que $$v_{1f}=v_{2i}\quad \text{y}\quad v_{2f}=v_{1i}$$ lo que significa que las partículas intercambian velocidades. Esto es aproximadamente lo que uno observa en las colisiones frontales de las bolas de billar. Si la partícula 2 está en reposo al inicio, las ecuaciones se convierten en \begin{align*}v_{1f}=\left(\frac{m_1-m_2}{m_1+m_2}\right)v_{1i}\quad \text{y}\quad v_{2f}=\left(\frac{2m_1}{m_1+m_2}\right)v_{1i}\end{align*}

Fig. 5. Colisión frontal de dos partículas idénticas con una en reposo.

Caso 2. Si $m_1\gg m_2$ esto es, cuando una partícula muy pesada choca frontalmente con una muy ligera que inicialmente está en reposo:\begin{align*}
v_{1f}\approx v_{1i}\quad \text{y}\quad v_{2f}\approx 2v_{1i}
\end{align*}Un ejemplo de tal colisión es la de un átomo pesado en movimiento, como el uranio, que golpea un átomo ligero, como el hidrógeno.

Fig. 6. Colisión frontal con $m_1\gg m_2$ y $v_{2i}=0$.

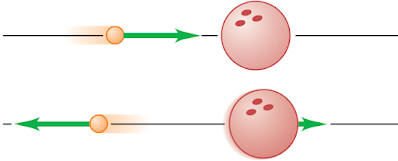
Caso 3. Si $m_2\gg m_1$ esto es, cuando una partícula muy ligera choca frontalmente con una muy pesada que inicialmente está en reposo:$$v_{1f}\approx -v_{1i}\quad \text{y}\quad v_{2f}\approx 0$$Un ejemplo de tal colisión ocurre cuando lanzamos una pelota de tenis contra una pared. La masa de la pared es extremadamente grande comparada con la masa de la pelota de tenis, lo que nos permite aplicar el mismo análisis.

Fig. 7. Colisión frontal con $m_2\gg m_1$ y $v_{2i}=0$.

Bibliografía

1. Lorenzo. (2017, agosto 9). Demostración experimental del principio de conservación de la cantidad de movimiento lineal (PCCML) y angular (PCCMA). Pendulo. Steemit. https://steemit.com/stem-espanol/@lorenzor/demostracion-experimental-del-principio-de-conservacion-de-la-cantidad-de-movimiento-lineal-pccml-y-angular-pccma-pendulo.
2. PhET Interactive Simulations. (n.d.). Collision Lab. University of Colorado Boulder. Recuperado de https://phet.colorado.edu/sims/html/collision-lab/latest/collision-lab_all.html.